矩阵

矩阵概念

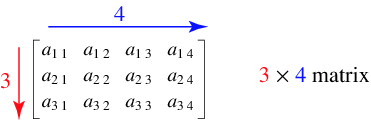
矩阵形式是一个数字表，以行和列的形式呈现：
$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}$
矩阵的行数m和列数n可以不相同，m行n列矩阵记为矩阵 $$A_{n \times m} 。

零矩阵和单位矩阵

mxn矩阵，如果所有元素都为0，则为零矩阵。
对于一个n阶方阵，如果主对角线元素全为1，其余元素都为0则称为n阶单位阵。

矩阵转置

转置操作即是将矩阵的行和列互换。
$A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix}\Rightarrow A^T = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \\ \end{bmatrix}$

矩阵运算

矩阵加减法

两个矩阵A和B要能执行加减法，必须是行和列数目相等的。
$\begin{bmatrix} 1 & 1 \\ 2 & 3 \\ \end{bmatrix} + \begin{bmatrix} 3 & 2 \\ 1 & 1 \\ \end{bmatrix} = \begin{bmatrix} 1+3 & 1+2 \\ 2+1 & 3+1 \\ \end{bmatrix} = \begin{bmatrix} 4 & 3 \\ 3 & 4 \\ \end{bmatrix}$

标量和矩阵乘法

用一个数k乘以矩阵A，结果为矩阵A中每个元素乘以数k。例如：
$2*\begin{bmatrix} 2 & 4 \\ 5 & 6 \\ \end{bmatrix} = \begin{bmatrix} 2*2 & 4*2 \\ 5*2 & 6*2 \\ \end{bmatrix} = \begin{bmatrix} 4 & 8 \\ 10 & 12 \\ \end{bmatrix}$

矩阵和矩阵乘法

两个矩阵$A_{m \times n}$和$B_{n \times p}$要执行乘法操作，需要满足：左边矩阵的列数和右边矩阵的行数相等，并且结果矩阵为$C_{m \times p}$。

$$\begin{bmatrix} c_{11} & c_{12} & \cdots & c_{1p}\\ c_{21} & c_{22} & \cdots & c_{2p}\\ \vdots &\vdots & \ddots & \vdots \\ c_{n1} & c_{n2} & \cdots & c_{np}\\ \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1m}\\ a_{21} & a_{22} & \cdots & a_{2m}\\ \vdots &\vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm}\\ \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1p}\\ b_{21} & b_{22} & \cdots & b_{2p}\\ \vdots &\vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \cdots & b_{mp}\\ \end{bmatrix}$$

其中C中第i行第j列的元素为：
$C_{ij} = \sum _{k = 1} ^{n} {a_{ik}b_{kj}}$
例如：
$\begin{bmatrix} a & b & c\\ d & e & f\\ \end{bmatrix} \begin{bmatrix} u & v \\ w & x \\ y & z \\ \end{bmatrix} = \begin{bmatrix} au+bw+cy & av+bx+cz \\ du+ew+fy & dv+ex+fz \\ \end{bmatrix}$

注意矩阵乘法不满足交换律$AB \ne BA$(当然存在特殊情况下相等)

矩阵和向量相乘

矩阵和向量相乘是矩阵和矩阵相乘的特例，给定矩阵A和列向量$\vec(v)$,相乘过程如下所示：
$A\vec{v} = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{bmatrix} \begin{bmatrix} -1 \\ 0 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 1*-1 + 2*0 + 3*1 \\ 4*-1 + 5*0 + 6*1 \\ 7*-1 + 8*0 + 9*1 \\ \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \\ 2 \\ \end{bmatrix}$

逆矩阵

对于n阶方阵A，如果存在一个n阶方阵B使得：
$AB = BA = I$
则称$B$是$A$的逆矩阵，这时就说矩阵$A$是可逆矩阵，或者说矩阵$A$是非奇异矩阵。单位矩阵$I$是主对角线上元素为1，其余元素都为0的n阶方阵。例如3x3的单位矩阵为
$I_{3 \times 3} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix}$
注意 只有n阶方阵才有逆矩阵的概念，对于一般的矩阵$A_{m \times n}(m \ne n)$不存在这样的矩阵$B$满足14式。

逆矩阵的应用意义

在3D图形处理中，用一个变换矩阵乘以向量，代表了对原始图形进行了某种变换，例如缩小，旋转等，逆矩阵标识这个操作的逆操作，也就是能够撤销这一操作。 $M^{-1}(M\vec{v}) = (M^{-1}M)\vec{v} = I\vec{v} = \vec{v}$ 注意转换矩阵应用顺序，当用矩阵A，B，C转换向量$\vec{v}$时，如果$\vec{v}$用行向量记法，则矩阵按转换顺序从左到右列出，表达式为$\vec{v}ABC$；如果$\vec{v}$采用列向量记法，则转换矩阵应该放在左边，并且从右往左发生，对应的转换记为$CBA\vec{v}$
$\vec{v} = \begin{bmatrix} -1 \\ 0 \\ 1 \\ \end{bmatrix} \Rightarrow CBA\vec{v}$
$\vec{v} = \begin{bmatrix} -1 & 0 & 1 \\ \end{bmatrix} \Rightarrow \vec{v}ABC$

正交矩阵

对于方阵$M$,当且仅当$M$与其转置矩阵$M^{T}$的成绩等于单位矩阵时，称其为正交矩阵。
$M正交 \Leftrightarrow MM^{T} = I \Leftrightarrow M^{T} = M^{-1}$
正交矩阵的一大优势在于，计算逆矩阵时，只需要对原矩阵转置即可，从而减少了计算量。3D图形中的旋转和镜像变换都是正交的。

正交矩阵举例

例如下面的矩阵$R_x(\theta)$表示物体绕x轴旋转$\theta$角度
$R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos\theta & -\sin\theta & 0\\ 1 & \sin\theta & \cos\theta & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}$
可以通过旋转矩阵本身的特性证明。对于旋转而言，绕x轴旋转$\theta$角度的逆操作等于绕x轴旋转$-\theta$度，因此：
$R_x(\theta)^{-1} = R_x(-\theta)$ $\cos(-\theta) = \cos\theta$ $\sin(-\theta) = -\sin\theta$ $R_x(-\theta) = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos\theta & \sin\theta & 0\\ 1 & -\sin\theta & \cos\theta & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}$ $R_x(-\theta) = R_x(\theta)^T$
由此可得$R_x(\theta)$为正交矩阵

计算机图形学中的矩阵

矩阵的几何功能

1.矩阵是一种线性变换
2.矩阵是一种映射，映射可以是一对一，也可以是一对多
3.矩阵是一种空间变换，每一种矩阵都是有本身的几何意义，而不是单纯的数字组合

线性变换

线性变换指的是可以保留矢量加和变量乘的变换。用数学公司来表示：
$f(x)+f(y) = f(x+y)$
$kf(x) = f(kx)$
缩放就是一种线性变换
$f(x) = 2x$
$f(x) + f(y) = 2x+2y = 2(x+y) = f(x+y)$
$kf(x) = 2(kx) = f(kx)$
如果要对三维的矢量进行变换，那么可以用3x3的矩阵表示所有的线性变换，例如缩放变换：
$\begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = \begin{cases} 2x + 0y + 0z \\ 0x - 2y + 0z \\ 0x + 0y + 2z \\ \end{cases} = \begin{bmatrix} 2x \\ 2y \\ 2z \\ \end{bmatrix}$ 但是平移变换不符合线性变换
$f(x) = x + 2$
$f(x) + f(x) = x + 2 + x + 2 = 2x + 4$
$f(x+x) = 2x + 2$
$f(x) + f(x) \ne f(x+x)$
所以为了支持平移变换，使用一个4x4的矩阵来表示3维空间的变换,因此我们需要把矢量扩展到四维空间下，就是所谓的齐次坐标系
$\begin{bmatrix} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x+2 \\ y+2 \\ z+2 \\ 1 \\ \end{bmatrix}$

矩阵变换的通式

$\begin{bmatrix} M_{3x3} & t_{3x1} \\ 0_{1x3} & 1 \\ \end{bmatrix}$
其中矩阵$M_{3x3}$用于便是旋转和缩放，$t_{3x1}$用于表示平移。

平移变换

对点进行平移变换：
$\begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x+t_x \\ y+t_y \\ z+t_z \\ 1 \\ \end{bmatrix}$ 对方向矢量进行平移变换：
$\begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 0 \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ 0 \\ \end{bmatrix}$ 因为矢量只有方向，没有位置，所以矢量的第四维为0，平移变换不会对矢量造成影响。PS:平移矩阵不是一个正交矩阵。

缩放矩阵

$\begin{bmatrix} k_x & 0 & 0 & 0 \\ 0 & k_y & 0 & 0 \\ 0 & 0 & k_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 0\\ \end{bmatrix} = \begin{bmatrix} k_xx \\ k_yy \\ k_zz \\ 0 \\ \end{bmatrix}$

旋转矩阵

绕x轴：
$R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$
绕y轴：
$R_x(\theta) = \begin{bmatrix} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$
绕z轴：
$R_x(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$
旋转矩阵是正交矩阵

复合变换

我们可以吧平移、旋转和缩放组合起来，形成一个复杂的变换过程。
列坐标表示： $P_{new} = M_{translation}M_{rotation}M_{scale}P_{old}$ 变换顺序为从右往左，即先缩放变换，再旋转变换，最后平移变换。 在大多数情况下，我们约定变换顺序是：先缩放，在旋转，最后平移。
为什么这么约定呢？假设先进行平移，在进行缩放，那之前的平移值也会被影响，从而导致效果和数值显示的不同。
我还需要注意小心旋转的变换顺序。在Unity中，旋转顺序是zxy。
旋转时还存在两种坐标系可以选择： Unity文档中说的选择顺序指的是在第一种情况下的顺序。

---

• ← Previous Post
• Next Post →