向量

向量的概念

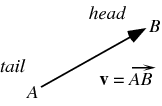
1.向量的大小就是向量的长度（模）。响亮的长度非负。
2.向量的方向描述了向量的朝向。
3.向量是没有位置的。

零向量与单位向量

向量的长度即模，定义为：
$\left|v\right| = \sqrt{v_1^2+v_2^2+...+v_n^2} 即 \left|v\right| = \sqrt{\sum_{i=1}^n v_i^2}$
模等于0的向量为零向量，模等于1的向量为单位向量。零向量的方向是任意的。 单位向量的计算方法:
$v_n = \frac{v}{\left|v\right|} , v\ne 0$

三角形法则和平行四边形法则

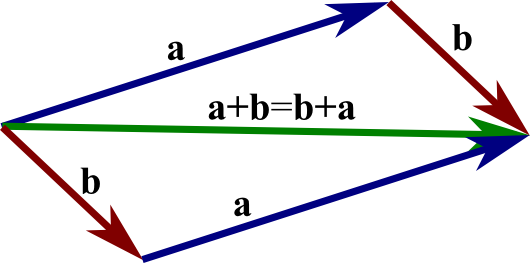
两个向量a和b，当将b的起点放在a的终点，连接a的起点和b的终点的向量成为向量a，b之和，记为：c = a + b,如下图所示： 平行四边形法则，表示的是向量加法运算的结合律，即：a+b = b+a,如下图所示：

向量夹角

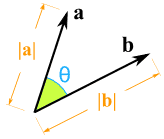
向量点积

向量点积也叫做向量的数量积，点积的结果是一个标量，其定义为：
$\vec{A}\cdot\vec{B} = \left|A\right|\left|B\right|\cos\theta（1）$

其中 $\theta$ 表示 $\vec{A}$ 和 $\vec{B}$ 之间的夹角 。

向量点积的几何意义

首先要了解向量的投影，向量$\vec{A}$在$\vec{B}$上的投影定义为：
$\vec{A_B} = \left|A\right|\cos\theta（2）$
如下图：

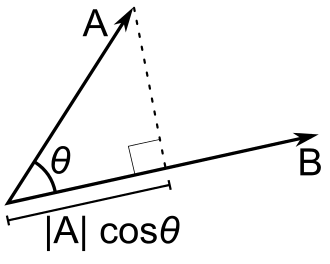
则（1）式可以写为：
$\vec{A}\cdot\vec{B} = \left|A\right|B_A = \left|B\right|A_B（3）$

向量点积的代数意义

设$\vec{A} = (x_1,y_1)$和$\vec{b} = (x_2,y_2)$，他们的点积为：
$\vec{A}\cdot\vec{B} = x_1x_2 + y_1y_2（4）$

向量几何定义推导代数定义

设$\vec{A} = (x_1,y_1)$和$\vec{b} = (x_2,y_2)$，根据向量坐标的意义可知： $\vec{A} = x_1\vec{i}+y_1\vec{j}$
$\vec{B} = x_2\vec{i}+y_2\vec{j}$
根据点积的分配律得： $\vec{A}\cdot\vec{B} = (x_1\vec{i}+y_1\vec{j}) \cdot (x_2\vec{i}+y_2\vec{j})$ $= x_1x_2\vec{i}\cdot\vec{i} + x_1y_2\vec{i}\cdot\vec{j} + y_1y_2\vec{j}\cdot\vec{j} + x_2y_1\vec{j}\cdot\vec{i}$
又
$\vec{i}\cdot\vec{i} = \vec{j}\cdot\vec{j} = 1$ $\vec{i}\cdot\vec{j} = 0$ 所以 $\vec{A}\cdot\vec{B} = x_1x_2 + y_1y_2（4）$

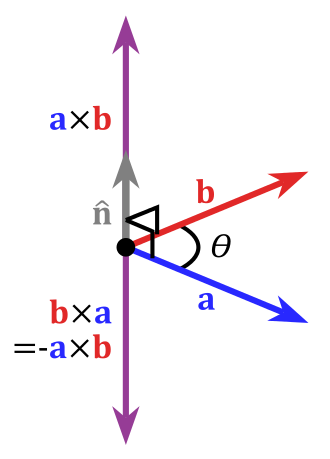
向量的叉积

两个向量$\vec{a}$和$\vec{b}$的叉积，结果是一个向量$\vec{c} = \vec{a}\times\vec{a}$,$\vec{c}$的方向垂直于$\vec{a}$和$\vec{b}$，它的方向根据右手定则来确定；$\vec{c}$的大小等于：
$\left|c\right| = \left|a\right|\left|b\right|\sin\theta$
叉积如下图所示：

向量叉积的代数意义

$\vec{a}\times\vec{b} = (a_yb_z-a_zb_y, a_zb_x - a_xb_z, a_xb_y - a_yb_x)$

• ← Previous Post
• Next Post →